Cyclic stress-strain behavior of structural steel with yield-strength up to 460 N/mm<sup>2</sup>

doi:10.1007/s11709-014-0245-y

Cite this article

Yiyi CHEN, Wei SUN, Tak-Ming CHAN. Cyclic stress-strain behavior of structural steel with yield-strength up to 460 N/mm² . Frontiers of Structural and Civil Engineering, 2014, 8(2): 178-186 Copy to clipboard

This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Cyclic stress-strain behavior of structural steel with yield-strength up to 460 N/mm²

Yiyi CHEN¹, Wei SUN², Tak-Ming CHAN³

1. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China

2. Architecture Design & Research Institute of Tongji University (Group) Co. Ltd., Shanghai 200092, China

3. School of Engineering, University of Warwick, Coventry CV4 7AL, UK

t.m.chan@warwick.ac.uk

Abstract

This paper presents a constitutive model based on Ramberg-Osgood equation to describe the hysteresis material behavior of structural carbon steel with nominal yield strength between 235 to 420 N/mm². The proposed model was calibrated against a series of cyclic material tests with strain amplitude varying from 0.5% to 2.0%. A simple relationship between the modular parameterK and the yield strengthf_y was proposed. The calibrated Ramberg-Osgood model revealed excellent agreement with the experimental results and captured further the experimental behavior of test specimens with nominal yield strength of 460 N/mm². The proposed constitutive model was also adopted in conjunction with the combined kinematic/isotropic materials description in ABAQUS to mimic a full scale experimental test under cyclic loading. The numerical results revealed close agreement with the experimental observations.

Keyword: constitutive model; finite element analysis; hysteresis curve; Ramberg-Osgood equation

Show Figures

Introduction

Ramberg and Osgood [ 1] first proposed an analytical formulation to describe the nonlinear behavior of material under compression and tension. Based on Ramberg and Osgood relations, numerous studies have been conducted to modify and improve the relationship to cover a wider range of strain for nonlinear materials under monotonic loads [ 2– 6] and to describe the stress-strain relationship at elevated temperature [ 7, 8]. Concerning hysteresis behavior, Skelton et al. [ 9] described the relationships between the various Masing-type models and the Ramberg-Osgood stress-strain response. A new link was established between the Ramberg-Osgood strength and cyclic hardening parameters. Broggiato et al. [ 10] also described the use of the Chaboche nonlinear kinematic hardening model for cyclic plasticity assessment. The tuned Chaboche model for elastoplastic material description was employed in the finite element simulation which was capable of following the cyclic elastoplastic response very closely up to large accumulated plastic strain levels. However, limited research [ 11] is conducted in the development of hysteresis stress-strain models based on Ramberg-Osgood relationships for structural carbon steel. This paper presents the calibration of the Ramberg-Osgood equations against a series of cyclic materials tests [ 12] and proposes a constitutive model to describe the material hysteresis performance.

Calibration

A series of experimental tests on steel coupons under monotonic and cyclic loadings were conducted by Chen et al. [12]. Mean measured dimensions and key results from direct tensile tests are summarized in Table 1. The specimens are categorized according to the material grade as shown in columns 1 and 2, measured yield strength, measured ultimate strength, ratio of yield to ultimate strengths and measured elongation are shown in columns 3 to 6 respectively. Further experimental details can be found in Chen et al. [ 12].

Tab.1 Mean measured dimensions and key results from direct tensile tests

For the cyclic material tests, three different loading protocols 1) cyclic ascend 2) cyclic alternate and 3) cyclic tensile were employed as shown in Fig. 1. As shown in Fig. 1(a), cyclic ascend is a loading protocol with an equal strain increment of+/‒0.005 for each five-cycle loading phase up to+/- 0.02 strain amplitude. cyclic alternate refers to the loading scheme as shown in Fig. 1(b) which is similar to cyclic ascend, except the second and third loading phases were interchanged. The loading scheme of cyclic tensile is indicated in Fig. 1(c). All loadings are in tension and it oscillates incrementally up to 0.08 strain amplitude. Previous research [ 12] revealed that the loading protocols in particular between cyclic ascend and cyclic alternate affected the hysteresis behavior but the effect is minimal. This paper primarily focuses on the hysteresis response from cyclic ascend and cyclic alternate loading protocols.

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.1 Cyclic loading protocols. (a) Cyclic ascend; (b) cyclic alternate; (c) cyclic tensile

Ramberg-Osgood model

The most commonly used expression to describe nonlinear material stress-strain behavior is that proposed by Ramberg and Osgood [ 1] as shown in Eq. (1).

ϵ = \frac{σ}{E} + {(\frac{σ}{K})}^{n}

(1)

where, σ and ϵ are engineering stress and strain, respectively, E is the material Young’s modulus which was taken as 2 × 10⁵ N/mm² in this study, n is a strain hardening exponent and K is a modular parameter. Grouping terms, Eq. (1) can be simplified to

\hat{y} = {(\frac{σ}{K})}^{n}

(2)

where

\hat{y} = ϵ - \frac{σ}{E}

The corresponding data pairs are σ_i and ϵ_i - σ_i/ E where i = 1, 2, 3, …….. k. Given that

y_{i} = ϵ_{i} - \frac{σ_{i}}{E}

(3)

{\hat{y}}_{i} = {(\frac{σ_{i}}{K})}^{n}

(4)

and adopting the least-square method, the target is to minimize the following function to obtain an optimum pair of modular parameter K and strain-hardening exponent n.

f (K, n) = \sum_{i = 1}^{k} {(y_{i} - {\hat{y}}_{i})}^{2}

(5)

From

{\begin{array}{l} \frac{\partial f (K, n)}{\partial K} = 0 \\ \frac{\partial f (K, n)}{\partial n} = 0 \end{array}

(6a)

It can be deduced

{\begin{array}{l} \frac{n}{K^{n + 1}} \sum_{i = 1}^{k} σ_{i}^{n} (y_{i} - {\hat{y}}_{i}) = 0 \\ \frac{1}{K^{n}} \sum_{i = 1}^{k} σ_{i}^{n} (\ln σ_{i} - \ln K) (y_{i} - {\hat{y}}_{i}) = 0 \end{array}

(6b)

As K and n are both nonzeros, Eq. (6)b can be further simplified to

{\begin{array}{l} \sum_{i = 1}^{k} σ_{i}^{n} (y_{i} - {\hat{y}}_{i}) = 0 \\ \sum_{i = 1}^{k} σ_{i}^{n} \ln σ_{i} (y_{i} - {\hat{y}}_{i}) = 0 \end{array}

(7)

For a given set of σ_i, ϵ_i ( i = 1,2,…., k), the corresponding K and n parameters can then be determined.

Cyclic stress-strain curves

From Chen et al. [ 12], typical hysteresis loops are shown in Fig. 2. The hysteresis loops for Group 1 specimens under cyclic ascend (1-1) and cyclic alternate (1-2) loading protocol are shown in Figs. 2(a) and 2(b) respectively.

In general, the hysteresis loops are bi-symmetric, therefore, to simplify the calibration process against Ramberg-Osgood equations, the hysteresis loops in the first quadrant (I) are calibrated and the calibration results are shown in Tables 2 to 8.

Tab.2 Group 1 specimens Ramberg-Osgood parameters

Tab.3 Group 2 specimens Ramberg-Osgood parameters

Tab.4 Group 3 specimens Ramberg-Osgood parameters

Tab.5 Group 4 specimens Ramberg-Osgood parameters

Tab.6 Group 5 specimens Ramberg-Osgood parameters

Tab.7 Group 6 specimens Ramberg-Osgood parameters

Tab.8 Group 7 specimens Ramberg-Osgood parameters

Tables 2 to 8 show the calibrated parameters for Group 1 to 7 specimens under cyclic ascend and cyclic alternate loading protocols at different amplitudes. The coefficient of determination r² between the experimental data and proposed hysteresis models are also tabulated.

As shown in the above tables, all coefficient of determination r² are close to 1 showing close relation between experimental data and Ramberg-Osgood equations. Under different strain amplitudes, for example in Group 7 specimens (Table 8), the modular parameter K remains fairly constant while the strain-hardening exponent, n increases with the strain amplitude.

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.2 Hysteresis loops for Group 1 specimens. (a) Cyclic Ascend (1-1); (b) cyclic alternate (1-2)

Proposed K‒ f_y relationship

A summary of modular parameters for hysteresis loops under cyclic ascend loading protocol is shown in Table 9.

Tab.9 Modular parameters for hysteresis loops

Tab.10 Modular parameter and yield strength relation

As shown in the table, under different imposed strain amplitude, the variation of modular parameter K is minimal, for example for specimen 2-1, the maximum modular parameter is 1071 MPa while the minimum modular parameter is 1003 MPa, so an average value was used. It is also observed that as the yield stress increases, the modular parameter K displays an increasing trend. It is therefore proposed a linear relationship between modular parameter K and yield strength as follows: $K = 1.79 f_{y} + 532.$

The predicted K values show good correlation with the experimental results as summarized in Table 10.

Constitutive model

Primary skeleton stress-strain curve

Based on the discussion from Section 2, the proposed constitutive model of cyclic stress-strain behavior is summarized as follows:

ϵ = {\begin{array}{l} \frac{σ}{E} + {(\frac{σ}{K})}^{n}, σ \geq 0 \\ \frac{σ}{E} - {(\frac{- σ}{K})}^{n}, σ < 0 \end{array}

(9)

where K and n can be evaluated based on the methodology as shown in Section 2.1 for cyclic ascend loading protocol.

Cyclic stress-strain curve

ϵ = {\begin{array}{l} \frac{σ - σ_{u}}{E} + {(\frac{σ - σ_{u}}{K})}^{n} + ϵ_{u}, l o a d i n g i e σ - σ_{u} > 0 \\ \frac{σ - σ_{u}}{E} - {(\frac{σ_{u} - σ}{K})}^{n} + ϵ_{u}, u n l o a d i n g i e σ - σ_{u} < 0 \end{array}

(10)

where σ_u, ϵ_u are the unloading reference point at each cycle, E is taken as 2 × 10⁵ MPa, K can be obtained from the relationship proposed in Eq. (8) and n can be defined by the approach in Halford and Morrow [ 13]. Hence, to define full hysteresis stress-strain behavior of structural carbon steel, two key parameters which are K and n are needed. The parameters K and n also depend on the strength of steel, and the latter changes significant with the increase of maximum strain.

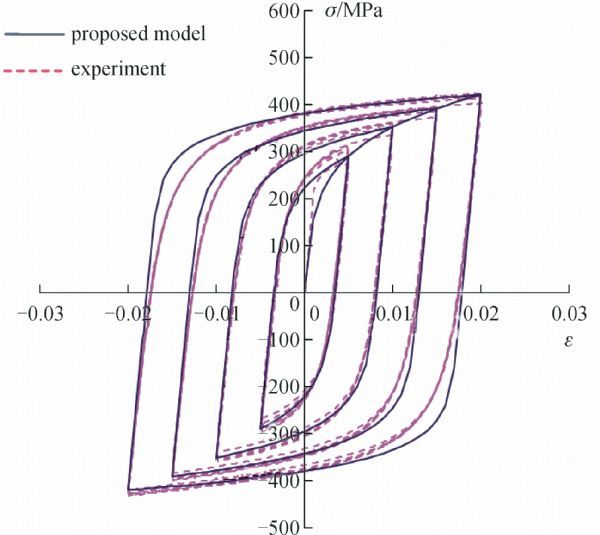
Based on Eqs. (9) and (10), the derived hysteresis stress-strain curves were compared with the experimental results. For Group 1 specimens, as shown before, the corresponding parameters are K = 1067 MPa (primary skeleton), n = 4.34 (primary skeleton), E = 2 × 10⁵ MPa and K = 1033 MPa (hysteresis behavior as shown in Table 10). For specimens under cyclic ascend loading protocol, the straining history is 0→0.005→-0.005→0.01→-0.01→0.015→-0.015→0.02→-0.02→0.02 and for specimens under cyclic alternate loading protocol, the straining history is 0→0.005→-0.005→0.015→-0.015→0.015→-0.01→0.01→-0.01→0.02→-0.02→0.02. The comparison between the proposed constitutive model and the experimental results are shown in Figs. 3 and 4.

The above figures revealed the proposed hysteresis models correlate closely with the experimental data. The proposed material stress-strain model can also capture the effect of different loading protocols. Figure 5 shows the hysteresis loops for Group 1 specimens under cyclic ascend (1-1) and cyclic alternate (1-2). The difference is indicated at strain amplitude of 0.01, the cyclic peak values for specimen 1-2 is greater than 1-1, which illustrates the effect of loading protocol but as discussed in Chen et al. [ 12], the effect is insignificant toward seismic applications.

In general, the calibrated Ramberg-Osgood equation shows excellent agreement with the experimental results on the primary skeleton and the cyclic stress-strain curves.

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.3 Hysteresis loops for Group 1 specimen under cyclic ascend loading protocol

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.4 Hysteresis loops for Group 1 specimen under cyclic alternate loading protocol

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.5 The effect of loading protocols on hysteresis loops

Application to Q460 specimens

The proposed constitutive model in Section 3 was calibrated by experimental coupons with nominal yield strengths between 235 to 420 MPa. To investigate their applicability to a higher grade of steel, this section presents the comparison between the proposed constitutive model and the experimental result on coupons with nominal yield strength of 460 MPa (Q460 specimens). The direct tensile tests from the additional Group 8 specimens were conducted by the Authors on Grade Q460E materials with the measured yield strength of 491 MPa, ultimate strength of 611 MPa, yield-ultimate strength ratio of 0.8 and the elongation of 22.7%. Other Group 9 specimens on Grade Q460C materials were tested by Shi et al. [ 14] with the reported yield strength of 466 MPa.

Based on the proposed constitutive models (Eqs. (8)‒(10)), Figs. 6 and 7 illustrate the comparison between the proposed models and the experimental observations which reveal close agreement between the two.

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.6 Hysteresis loops for Group 8 specimen under cyclic ascend loading protocol

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.7 Hysteresis loops for Group 9 specimen under cyclic ascend loading protocol

Numerical validation

This section presents a numerical study based upon the proposed constitutive model in Section 3.

Validation experiment

The validation experiment refers to a cyclic test of tubular column of steel grade Q235B with nominal yield strength of 235 N/mm². The geometry of the test arrangement is shown in Fig. 8. The bottom part of the specimen was anchored to the strong floor facilities at the Structures laboratory of Tongji University. The loading was applied through the top part of the specimen under displacement-controlled loading scheme. The loading scheme (Displacement ratio Δ/Δ₁ vs. number of cycle n) is shown in Fig. 9 which is similar to the cyclic ascend loading protocol as shown in Fig. 1(a). As shown in Fig. 9, Δ₁ (0.7 mm) is the yield displacement. Further experimental details are presented in Zhao et al. [ 15].

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.8 Specimen dimension (in mm)

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.9 Loading protocol

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.10 Finite element model

Numerical simulation

A numerical modeling investigation, employing the finite element (FE) package ABAQUS [ 16], was carried out to replicate the experimental results based on the proposed constitutive model in Section 3. The element chosen for the FE model was a general purpose linear brick element, with reduced integration, designated as C3D8R in the ABAQUS element library. The mesh density was carefully chosen by carrying out a mesh convergence study with the aim of achieving accurate results while minimizing computational effort. The meshed finite element model is shown in Fig. 10.

The true material stress-strain relationships were generated from the engineering stress-strain curves obtained from the tensile coupon tests and cyclic coupons [ 12]. A kinematic/isotropic combined model [ 16] was employed in which the kinematic hardening parameters employed were determined through the full stress-strain response of specimen 1-1 from Eqs. (8) and (9) under four different strain amplitudes. Boundary conditions were applied to the model fixed end support conditions at both ends but allowing free vertical displacement at the top. The vertical displacement at top end was monitored throughout the analysis. Geometric and material nonlinearity was incorporated in the models which also enabled the cyclic behavior to be traced. The numerical derived hysteresis curves are shown in Fig. 11 and are compared with the corresponding experimental hysteresis results. Replication of test results was found to be satisfactory with the numerical models able to successfully capture the initial primary stress-strain behavior and general hysteresis response.

	Figure Option View Download New Window Download As Powerpoint Slide
	Fig.11 Hysteresis loops.

Conclusions

This paper proposes a constitutive model based on Ramberg-Osgood equations to describe the primary skeleton stress-strain behavior and the cyclic stress-strain response for structural carbon steel with yield strength up to 420 N/mm². The proposed model was calibrated against a series of cyclic material tests with nominal yield strength between 235 to 420 N/mm² which revealed close agreement between the proposed model and the experimental results. A linear relation between modular parameter K and yield strength f_y was also proposed. Two key parameters K and n were defined which were used to describe the full stress-strain response under cyclic load. The proposed model was also able to capable the material hysteresis performance of coupons with nominal yield strength of 460 N/mm². The proposed constitutive model was then employed in a numerical validation which has showed excellent agreement between the numerical and the experimental results. This research forms part of an on-going research program at Tongji University to investigate the material hysteresis response of structural carbon steel with strain amplitude up to 10%.

References

View Option

1	Ramberg W, Osgood W R. Description of stress-strain curves by three parameters. National Advisory Committee for Aeronautics, Technical Note No. 902, 1943 [Cited within: 2]
2	Mirambell E, Real E. On the calculation of deflections in structural stainless steel beams: An experimental and numerical investigation. Journal of Constructional Steel Research, 2000, 54(1): 109–133 [Cited within: 1] [JCR: 1.327]
3	Rasmussen K J R. Full-range stress-strain curves for stainless steel alloys. Journal of Constructional Steel Research, 2003, 59(1): 47–61 [Cited within: 1] [JCR: 1.327]
4	Gardner L, Nethercot D A. Experiments on stainless steel hollow sections. Part 1: Material and cross-sectional behaviour. Journal of Constructional Steel Research, 2004, 60(9): 1291–1318 [Cited within: 1] [JCR: 1.327]
5	Gardner L, Ashraf M. Structural design for nonlinear metallic materials. Engineering Structures, 2006, 28(6): 926–934 [Cited within: 1] [JCR: 1.713]
6	Quach W M, Teng J G, Chung K F. Three-stage full-range stress-strain model for stainless steels. Journal of Structural Engineering, 2008, 134(9): 1518–1527 [Cited within: 1]
7	Chen J, Young B. Effects of elevated temperatures on the mechanical properties of cold-formed steel. Proceedings in the International symposium on cold formed steel metal structures, 2004, 139–158 [Cited within: 1]
8	Chen J, Young B. Stress-strain curves for stainless steel at elevated temperatures. Engineering Structures, 2006, 28(2): 229–239. DOI:10.1016/j.engstruct.2005.07.005 [Cited within: 1] [JCR: 1.713]
9	Skelton R P, Maier H J, Christ H J. The Bauschinger effect, Masing model and the Ramberg-Osgood relation for cyclic deformation in metals. Materials Science and Engineering, 1997, 238(2): 377–390 [Cited within: 1]
10	Broggiato G B, Campana F, Cortese L. The Chaboche nonlinear kinematic hardening model: Calibration methodology and validation. Meccanica, 2008, 43(2): 115–124 [Cited within: 1] [JCR: 1.747]
11	Shi G, Wang M, Bai Y, Wang F, Shi Y J, Wang Y Q. Experimental and modeling study of high-strength structural steel under cyclic loading. Engineering Structures, 2012, 37: 1–13 [Cited within: 1] [JCR: 1.713]
12	Chen Y Y, Sun W, Chan T M. Effect of loading protocols on the hysteresis behaviour of structural carbon steel with yield strength up to 460 N/mm². Advances in Structural Engineering, 2013, 16(4): 707–719 [Cited within: 6] [JCR: 0.489]
13	Halford G R, Morrow J. Low-cycle fatigue in torsion. Proceedings of the American Society for Testing and Materials, 1962, 62: 695–709 [Cited within: 1]
14	Shi G, Ban H Y, Shi Y J, Wang Y Q. Engineering application and recent research progress on high strength steel structures. Industrial Construction, 2012, 42(1): 1–7 (in Chinese) [Cited within: 1] [CJCR: 0.566]
15	Zhao X Z, Ge L J, Chen Y Y, He M X. Research on the effect of assembling weld form on mechanical behavior of box brace. Journal of Building Structures, 2008, 29(3): 88–95 (in Chinese) [Cited within: 1] [CJCR: 1.074]
16	ABAQUS. Analysis User’s Manual I–V. Version 6. 7. USA: ABAQUS, Inc, 2007 [Cited within: 2]

1943

0.0

... IntroductionRamberg and Osgood [1] first proposed an analytical formulation to describe the nonlinear behavior of material under compression and tension ...

... Ramberg-Osgood modelThe most commonly used expression to describe nonlinear material stress-strain behavior is that proposed by Ramberg and Osgood [1] as shown in Eq ...

2000

1.327

0.0

... Based on Ramberg and Osgood relations, numerous studies have been conducted to modify and improve the relationship to cover a wider range of strain for nonlinear materials under monotonic loads [2–6] and to describe the stress-strain relationship at elevated temperature [7,8] ...

2003

1.327

0.0

2004

1.327

0.0

. 2004, 60(9):1291-1318 DOI:10.1016/j.jcsr.2003.11.006

Experiments on stainless steel hollow sections. Part 1: Material and cross-sectional behaviour

Abstract

Basic material properties and cross-sectional data (stress–strain curves and load–end shortening curves) are presented for square, rectangular and circular hollow section specimens in Grade 1.4301 stainless steel. The material tests cover flat material in tension and in compression as well as corner material in tension. Modifications to the Ramberg–Osgood representation are suggested to ensure a close fit to both tensile and compressive behaviour over the full range of strains of interest. Results, including full load–end shortening curves, for a total of 37 stub column tests have been presented. The results have been used to develop an explicit relationship between cross-sectional slenderness and cross-sectional deformation capacity, which forms the basis for a proposed new design approach for stainless steel structures.

2006

1.713

0.0

. 2006, 28(6):926-934 DOI:10.1016/j.engstruct.2005.11.001

Structural design for nonlinear metallic materials

Abstract

The material stress–strain behaviour of structural carbon steel may be suitably accurately reflected for design purposes by an idealised elastic, perfectly-plastic material model; such material behaviour lends itself to the concept of section classification. There are, however, a number of structural materials, such as aluminium, stainless steel and some high strength, cold-worked steels, where this idealised model becomes inaccurate due to non-linearity of the stress–strain response below the yield point and considerable strain hardening beyond the yield point. Resulting design methods, developed on the basis of the idealised material behaviour, are necessarily overly conservative. A new method has been developed that utilises a more accurate material model and a continuous measure of cross-section deformation capacity (rather than the discretised system of section classification) to provide more rational and efficient designs. This paper describes the basis for the proposed design method and presents a comparison with results obtained from laboratory testing and those predicted by the current Eurocode approach. The proposed design method offers average increases in member resistances of around 20% over the current Eurocode approach, and a reduction in scatter of the prediction.

2008

0.0

2004

0.0

2006

1.713

0.0

. 2006, 28(2):229-239 DOI:10.1016/j.engstruct.2005.07.005

Stress-strain curves for stainless steel at elevated temperatures

Abstract

This paper presents the mechanical properties data of stainless steel at elevated temperatures. Accurate prediction of the material properties of stainless steel at elevated temperatures is necessary for determining the load-carrying capacity of structures under fire conditions. However, full utilization of the special feature of stainless steel has not been possible due to lack of technique data on the fire resistance of stainless steel structural material. Therefore, both steady and transient tensile coupon tests were conducted at different temperatures ranging from approximately 20 to 1000 ^°C to obtained the material properties of stainless steel types EN 1.4462 (Duplex) and EN 1.4301 (AISI 304) with plate thickness of 2.0 mm. The elastic modulus, yield strength obtained at different strain levels, ultimate strength, ultimate strain and thermal elongation versus different temperatures are also plotted and compared with the prediction from the Australian, British and European standards. The test results obtained from this study are also compared with the test results predicted by other researchers. A unified equation for yield strength, elastic modulus, ultimate strength and ultimate strain of stainless steel at elevated temperatures is proposed in this paper. It is shown that the proposed equation accurately predicted the yield strength, elastic modulus, ultimate strength and ultimate strain compared with the test results. Furthermore, stress–strain curves at different temperatures are plotted and a stress–strain model is also proposed.

1997

0.0

... [9] described the relationships between the various Masing-type models and the Ramberg-Osgood stress-strain response ...

2008

1.747

0.0

. 2008, 43(2):115-124 DOI:10.1007/s11012-008-9115-9

The Chaboche nonlinear kinematic hardening model: Calibration methodology and validation

1.University of Rome “La Sapienza” Department of Mechanics and Aeronautics via Eudossiana 18-00184 Rome Italy<br/>

This work studies how a nonlinear kinematic model aimed for cyclic plasticity could be put into effect and used within a FEM code. A correct modeling of cyclic elasto-plastic behavior can be exploited in low-cycle fatigue life investigation as well as in manufacturing problems related to springback prediction. The chosen formulation has been proposed by Chaboche, and it is implemented in most of the commercial codes used for nonlinear FEM simulations. At first, a procedure for the proper identification of unknown material model parameters has been put forward. This calibration, based on the data collected from experimental low-cycle fatigue tests, has been performed by means of an inverse method. Laboratory tests differ according to the type of material under investigation. A classification can be operated distinguishing between specimens obtained from bulk materials or from sheet metals. For the former, standard tension-compression tests have been performed, while for the latter, a dedicated testing equipment for three-point bend cyclic tests has been devised. Then, further experimental tests have been run to check model transferability: different strain per cycle amplitudes, asymmetric strain cycling and different stress triaxiality levels have been investigated. For each of these tests, experimental vs. FEM results have been analyzed to show the level of agreement that has been reached.

... [10] also described the use of the Chaboche nonlinear kinematic hardening model for cyclic plasticity assessment ...

2012

1.713

0.0

... However, limited research [11] is conducted in the development of hysteresis stress-strain models based on Ramberg-Osgood relationships for structural carbon steel ...

2013

0.489

0.0

... This paper presents the calibration of the Ramberg-Osgood equations against a series of cyclic materials tests [12] and proposes a constitutive model to describe the material hysteresis performance ...

... [12] ...

... Previous research [12] revealed that the loading protocols in particular between cyclic ascend and cyclic alternate affected the hysteresis behavior but the effect is minimal ...

... [12], typical hysteresis loops are shown in Fig ...

... [12], the effect is insignificant toward seismic applications ...

... The true material stress-strain relationships were generated from the engineering stress-strain curves obtained from the tensile coupon tests and cyclic coupons [12] ...

1962

0.0

... (8) and n can be defined by the approach in Halford and Morrow [13] ...

2012

0.0

0.566

... [14] with the reported yield strength of 466 MPa ...

2008

0.0

1.074

. 2008, 29(3):88-95

Research on the effect of assembling weld form on mechanical behavior of box brace

Both monotonic axial compressive and axially loaded cyclic tests have been carried out on the steel box brace used in New CCTV Building to investigate the effect of assembling welds including full penetration and partial penetration on the structural behavior of the brace.Numerical analyses simulating the static and cyclic behavior were also conducted by utilizing the general-purpose FEM package ABAQUS.The contact development between the un-welded surfaces of the partial penetration weld was analyzed in details.Both experimental and FE analytical results show that partial penetration weld can be used in members of New CCTV Building with a width-to-thickness ratio of 10.Furthermore,parameter analyses including width-to-thickness ratio,eccentric loading and residual stresses indicate that,for braces,with a width-to-thickness ratio less than 20 and subject to axial compressive loading,as well as those with a width-to-thickness ratio no more than 10 and subject to eccentric loading,partial penetration continuous weld can be used in the built-up box section connection between flanges and webs.

为考察全熔透和部分熔透两种组装焊缝形式对箱形截面钢支撑受力性能的影响,本文对中央电视台新台址建设工程中的箱形截面支撑进行了单调受压、轴向反复拉压试验;同时,采用ABAQUS有限元软件实现了对部分熔透试件未熔透处的接触模拟和滞回性能模拟。试验与有限元分析结果表明,中央电视台新台址工程中宽厚比为10的板件可采用部分熔透的组装焊缝形式。考虑板件宽厚比、偏心加载以及残余应力的参数分析结果表明,板件宽厚比小于20的轴心受压支撑以及板件宽厚比不大于10的偏心受力支撑中,箱形截面翼缘与腹板的连接可采用部分熔透的连续焊缝。

... [15] ...

2007

0.0

... Numerical simulationA numerical modeling investigation, employing the finite element (FE) package ABAQUS [16], was carried out to replicate the experimental results based on the proposed constitutive model in Section 3 ...

... A kinematic/isotropic combined model [16] was employed in which the kinematic hardening parameters employed were determined through the full stress-strain response of specimen 1-1 from Eqs ...